Factorized Higher-Order CNNs with an Application to Spatio-Temporal Emotion Estimation, CVPR 2020

CVPR 2020

Antoine Toisoul*, Jean Kossaifi*, Adrian Bulat, Yannis Panagakis,

Tim Hospedales, Maja Pantic (* Joint First Authors)

Samsung AI Center, Imperial College London

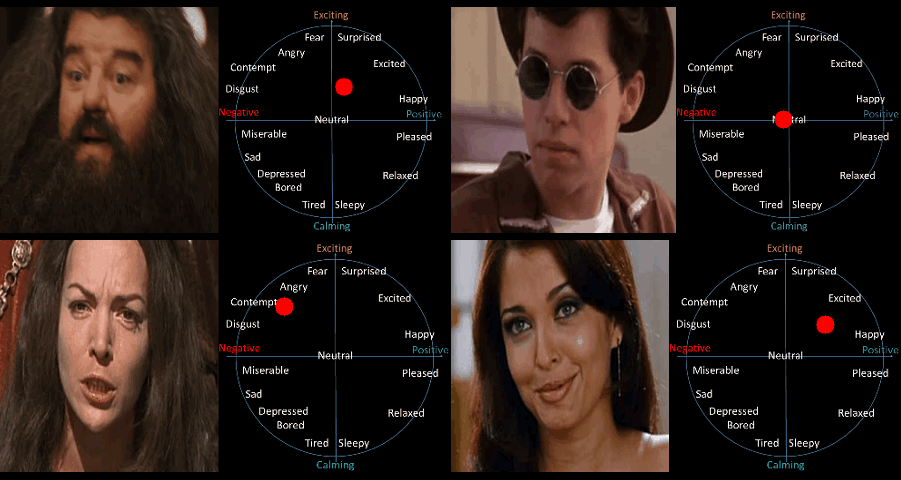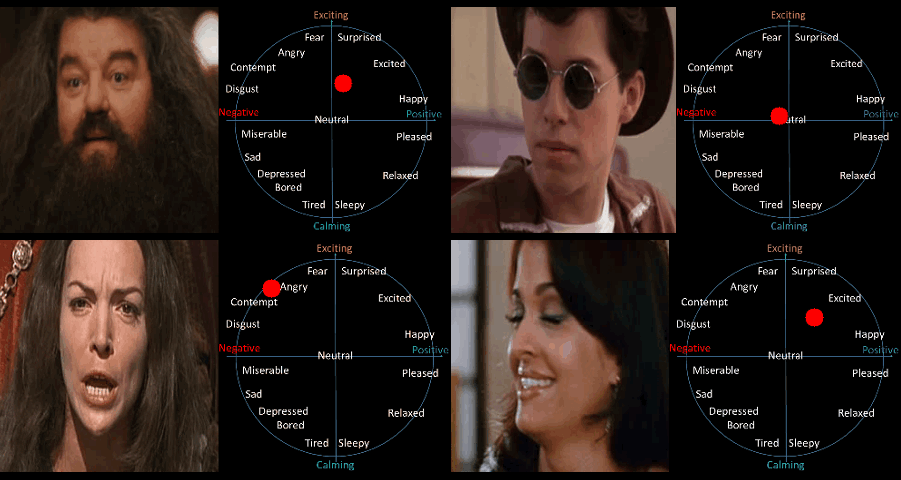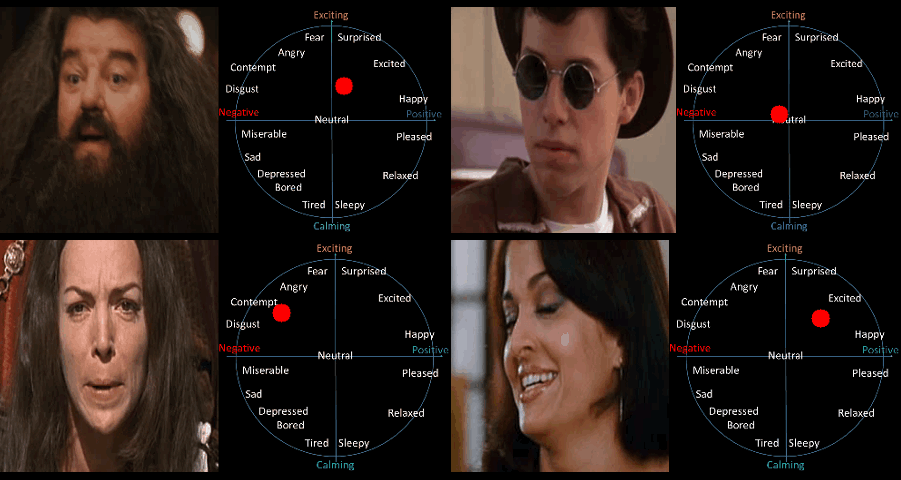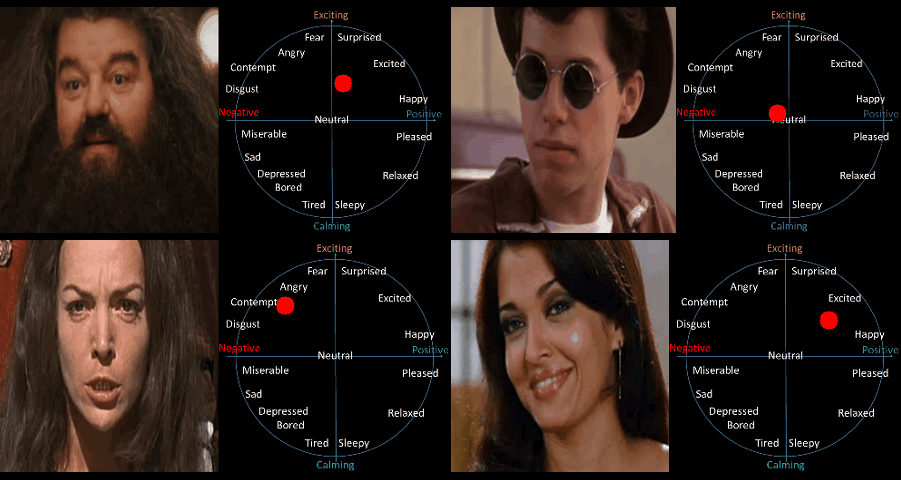
Figure 1 : Estimation of continuous emotions on videos using a spatio-temporal network trained with the transduction algorithm.

On the circumplex the x-axis corresponds to valence, i.e. how positive or negative the emotion is, and the y-axis corresponds to arousal, i.e. how calming or exciting the emotion is.

Publication: Factorized Higher-Order CNNs with an Application to Spatio-Temporal Emotion Estimation. Antoine Toisoul*, Jean Kossaifi*, Adrian Bulat, Yannis Panagakis, Tim Hospedales, Maja Pantic (* Joint First Authors), CVPR 2020

---

Abstract

Training deep neural networks with spatio-temporal (i.e., 3D) or multidimensional convolutions of higher-order is computationally challenging due to the millions of unknown parameters across dozens of layers. To alleviate this, one approach is to apply low-rank tensor decompositions to convolution kernels in order to compress the network and reduce its number of parameters. Alternatively, new convolutional blocks, such as MobileNet, can be directly designed for efficiency. In this paper, we unify these two approaches by proposing a tensor factorization framework for efficient multidimensional (separable) convolutions of higher-order. Interestingly, the proposed framework enables a novel higher-order transduction, allowing to train a network on a given domain (e.g., 2D images or N-dimensional data in general) and using transduction to generalize to higher-order data such as videos (or (N+K)-dimensional data in general), capturing for instance temporal dynamics while preserving the learnt spatial information.
We apply the proposed methodology, coined CP-Higher-Order Convolution (HO-CPConv), to spatio-temporal facial emotion analysis. Most existing facial affect models focus on static imagery and discard all temporal information. This is due to the above-mentioned burden of training 3D convolutional nets and the lack of large bodies of video data annotated by experts. We address both issues with our proposed framework. Initial training is first done on static imagery before using transduction to generalize to the temporal domain. We demonstrate superior performance on three challenging large scale affect estimation datasets, AffectNet, SEWA, and AFEW-VA.

Challenges when training higher-order networks

There are several issues when training higher-order networks (e.g., spatio-temporal 3D networks or higher-order) :

• slow training caused by expensive N-D convolutions

• N-D convolutions have many parameters to be learnt, therefore requiring a lot more data to be trained.

The goal of this paper is to tackle these two issues and simplify the training of higher-order networks. In particular, we show how this applies to the case of videos with spatio-temporal networks.

CP tensor decompositions

Tensors are a generalization of matrices to higher dimensions. They are the common data structure used in deep learning and at the core of the convolution operation employed in convolutional neural networks. It is therefore important to have efficient ways of representing tensors in order to decrease the memory requirements and computational cost of neural networks, especially when dealing with high-order convolutional neural networks.

In this paper, we propose to employ tensor factorizations in convolutional neural networks in order to reduce the number of parameters of higher-order convolutions and make their training easier.

Note that I will only describe the canonical decomposition (also denoted CP decomposition) here, but our tensor framework we also takes into account the Tucker decomposition and show how the convolutional blocks employed by common neural network architectures (e.g., ResNet bottleneck blocks or MobileNet blocks) are special cases of such tensor decompositions. Please refer to the full paper for the mathematical details.

The CP tensor decomposition allows to approximate a tensor of rank R with a sum of R rank-1 tensors. An example on an order 3 tensor is shown in Figure 2.

Figure 2 : CP factorization of an order 3 tensor. The tensor X is approximated as a sum of R rank-1 tensors. Figure taken from [1].

In particular, this means that in a convolutional neural network, N-D convolutional filters can approximated by a sum of sequential one dimensional convolutions along each dimension (also known as a separable convolution). Such decompositions therefore reduce the overall computational cost of high-dimensional convolutions. For instance, in the spatio-temporal case, a 3D separable convolution is obtained by the sequential application of a 1D convolution on the columns of the tensor, then by a 1D convolution on its rows and finally by a 1D convolution on the temporal dimension.

Unfortunately, unlike matrices, there is no algorithm to determine the rank of a tensor of order 3 or more as it is a NP-hard problem [1]. Therefore when applying tensor decompositions to neural networks, the rank of the decomposition is usually a hyperparameter. Fortunately, our tensor framework allows the network learn end-to-end the rank of each convolution operation when training the neural network (see below).

Transduction

The separability property of the CP decomposition is very important for spatio-temporal networks as it allows to learn a task on images and then to generalize to video via our novel transduction algorithm.

The transduction algorithm works as follows. Firstly, a 2D network in which every convolution is CP factorized is trained on static images. When the network has reached a good performance on static images, we add a temporal factor to the convolutions (the green factor in the image) in order to transform a 2D static network into a 3D spatio-temporal one. The new temporal factors are initialized to a constant value of one in order to compute an average of the previous and next frames. Note that the spatial factors have already been optimized to solve the task. Therefore, we keep them fixed and only backpropagate through the temporal factors until the network reaches a performance similar to the performance it had in the static case. Finally, when the temporal factors have been optimized, we jointly fine tune both the spatial and temporal factors to further optimize the performance of the network and learn the spatio-temporal dynamics more accurately.

Rank selection

As we saw earlier, a common question that arises when employing tensor decompositions is how to choose the rank of each CP convolution (i.e. the number of rank-1 tensors in the decomposition). In our case, we first choose the rank of each decomposition so that the number of parameters approximately matches the number of parameters of the original 2D convolution. During training, we apply a LASSO regularization on the weights of the CP decomposition (L1 norm added to the loss function) in order to obtain a sparse set of weights (the LASSO regularization leads to unimportant features being set to zero). Therefore, the network automatically learns end to end what rank it should employ for each convolution inside the network.

Sparsity induced by the LASSO regularization on a ResNet-18 for two values of the regularization parameter. Each residual block is shown on the graph for clarity. Note how 8 to 15% of the parameters can be removed from the network after training.

Thanks to the transduction, our spatio-temporal networks do not have more parameters than regular 2D CNNs as shown here :

• ResNet-18 2D CP : 11.1 million
• ResNet-18 2D CP : 11.1 million
• ResNet-18 CP 3D (after transduction) : 11.3 million
• ResNet-18 CP 3D (with LASSO 0.01) : 10.6 million
• ResNet-18 CP 3D (with LASSO 0.05) : 10 million

Finally, note that although we focused on the case of transferring knowledge from images to video, i.e 2D to 3D data, such idea could be employed to progressively transfer knowledge from N dimensions to N+K dimensions.

Results

We present results on three datasets designed for emotion recognition, namely AffectNet (static dataset), SEWA and AFEW-VA (video datasets). The task is to evaluate continuous emotions in terms of valence and arousal values. Valence and arousal are two continuous variables in the range [-1;1] that describe the wide range of emotions that can be displayed by humans on a daily basis. Valence gives how positive or negative an emotion is and arousal tells how exciting or calming the emotional display is. At such task, four metrics are commonly employed to evaluate an emotion recognition algorithm : the Root Mean Square Error (RMSE - which must be minimized), the Sign Agreement metric (SAGR - which must be maximized), the Pearson Correlation Coefficient (PCC - which must be maximized) and the Concordance Correlation Coefficient (CCC - which must be maximized).

For each dataset, we report that our CP decomposed networks give state of the art results at the task of recognizing emotions from static images. In particular, for SEWA and AFEW-VA, which contain video data (unlike AffectNet), we further apply our transduction algorithm to recognize emotions on video data and we report that the spatio-temporal networks trained with transduction reach a new state of the art. Please refer to the paper and supplementary document for additional experiments and details.

View fullsize

References

[1] Kolda, T. G., & Bader, B. W. (2009). Tensor decompositions and applications. SIAM review, 51(3), 455-500.